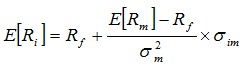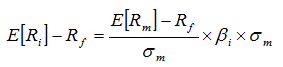Capital Asset Pricing Model

Parallèlement aux développements de la théorie financière relative aux portefeuilles boursiers , Il existe une relation entre la rentabilité espérée sur une action i (ou un portefeuille i) et sa covariance (im) avec le marché (m):

où

• Ri : Rendement de l’action i
• Rf : Rendement de l’actif sans risque de référence
• Rm : rendement du marché
• sigma carré m : Variance du rendement de marché
• sigma i m : Covariance entre le rendement de marché et celui de l’action i
• E(Ri) : Espérance mathématique du rendement de l’action i

Le ratio covariance/variance des rentabilités, communément appelé Bêta, peut être mis en évidence. On peut alors écrire

Le risque qui est rémunéré n’est pas le risque total de l’action, c’est son risque systématique : Bêta * sigma, ou en d’autres termes le risque non diversifiable.

Ainsi, tout investisseur qui sera prêt à courir un risque plus élevé devrait obtenir une rentabilité plus forte qui n’intégrera que le risque systématique qu’il assumera, et non le risque diversifiable. On peut à partir de cette formule évaluer le taux de rentabilité exigé k, apparu dans les calculs d’évaluation :

= taux sans risque + (prime de risque) * facteur Bêta